This little guide shows some possible solutions to solve the first levels for complexity and speed (not necessarily at the same time), and includes some explanations about the algorithms used.
 
 

1-1 Switch Assembly

 
No difficulty here, just follow the tutorial.
 
 
 

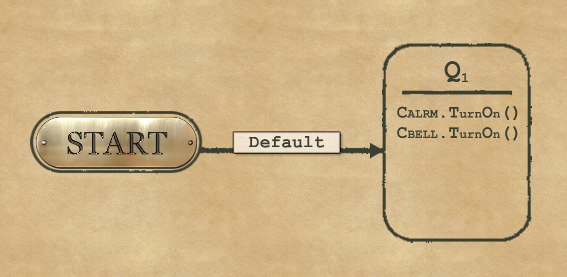
1-2 Westminster Quarters

 
No difficulty here, just follow the tutorial.
 
 
 

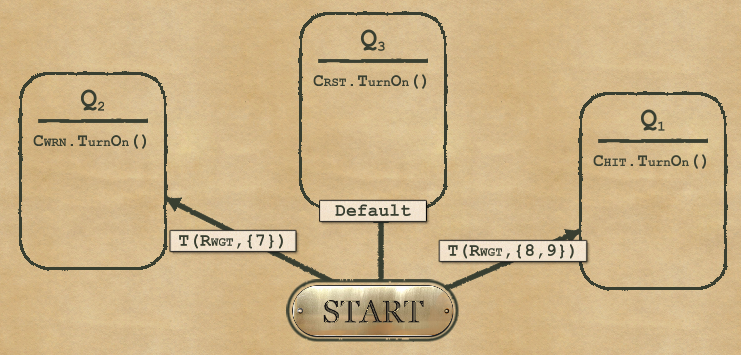
1-3 Chime Selector

 
A node has a high complexity (30 points) so avoid using too many nodes if you’re trying to solve the Complexity challenge. In this puzzle there are only 4 different tones, so you need only 4 nodes.
 
 
A transition costs 10 points no matter how complex it is, be it a “default” or a test with multiple AND conditions. So use them a lot if you want to reduce complexity.
 
 
For this puzzle, it’s mostly a matter of setting the right conditions on the transitions between nodes.
 
 
 

1-4 Control Valve

 
No difficulty here, just follow the tutorial.
 
 
 

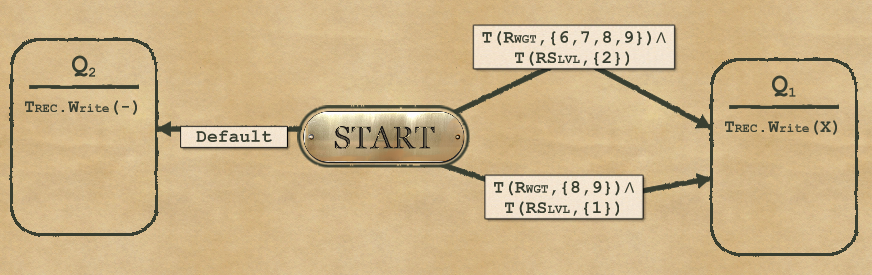
1-5 Recorder

 
There are only 2 possible actions: write X, or write –
 
That means 2 nodes. Then you can add the conditions, and you can even add several conditions that link the same nodes (this creating an OR condition).
 
 
 

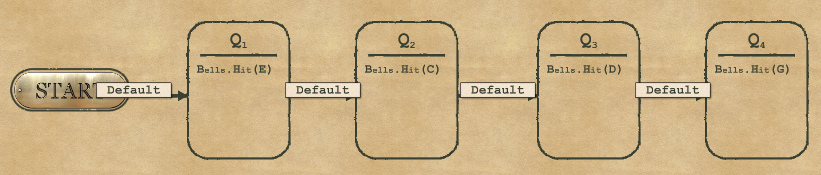
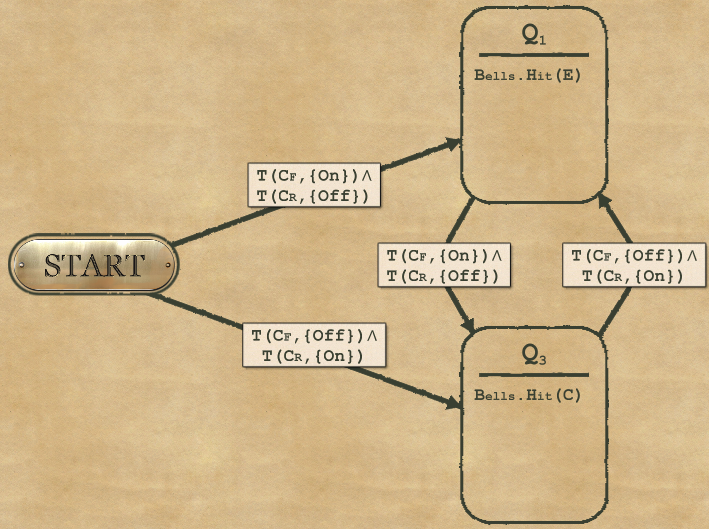
1-6 Welcome Chimes

 
Same kind of puzzle as before: there are only 2 actions to perform: ring C or ring E.
 
The fact that they have to be used in different order can be managed with conditions reduces the complexity score.
 
 
Oh, and if no condition matches nothing happens and the test case ends. So the “Otherwise, do nothing” requirement is actually automatically handled by… doing nothing.
 
 
 

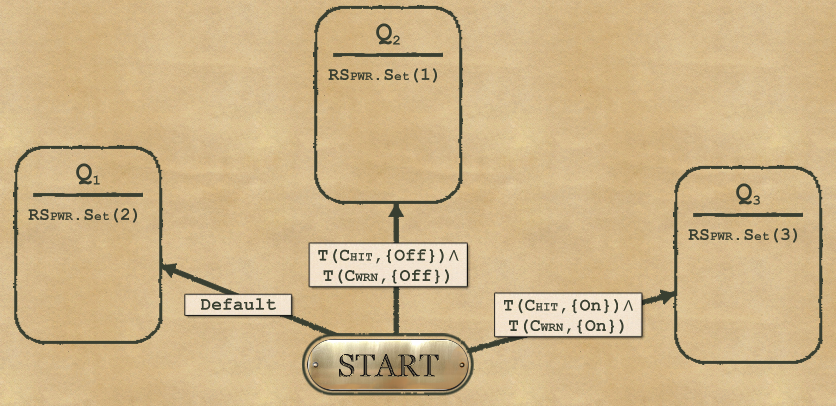
1-7 Automatic Transmission

 
Same as 1-4 : three possible states, so three nodes. The rest is conditions to reach them.
 
 
 

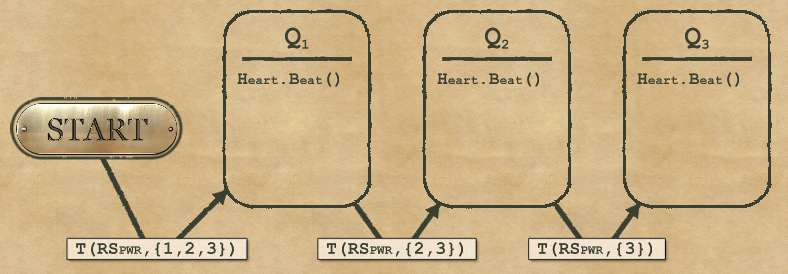
1-8 Heartbeat Compressor

 
Here the most complex case is to perform 3 heartbeats (the other cases requires less heartbeats). With the tools at your disposal at this stage of the game, you can’t perform any iteration/loop. So if you try with only a single node, you won’t be able to keep track of how many heartbeats you’ve already done and therefore won’t be able to stop at the right time. So only option is to set the 3 heartbeats in 3 nodes and setting the right conditions.
 
 
 

2-1 Cable Release

 
Straightforward solution meeting both Complexity and Speed requirements at the same time. The array always starts in position 1 (starting from the right). To reach the 3rd position we therefore need to go left twice. Then turn it on.
 
 
 

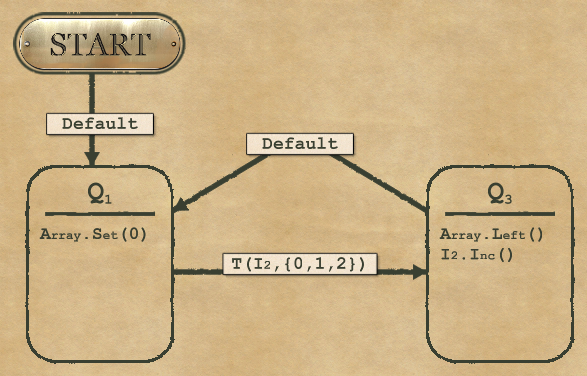
2-2 Resetter

For complexity, you have to play with the option of setting multiple actions in the same node. You can’t set multiple actions on the same device, but you can perform actions on different devices. In this case, you can increase the counter and move to the next position at the same time (in node Q3 on the figure)
 
 

 
 
For Speed, you need to minimize the steps performed during the execution of your tests. This is achieved by:
 

• Avoiding the integrator: there is only 4 positions in the array and the number of nodes is not important for Speed, so avoid taking time/steps to increase the integrator and test its values.
• Avoiding setting to 0 a value which is already 0. So use a condition to check if it’s useful first.

 

 
 
 

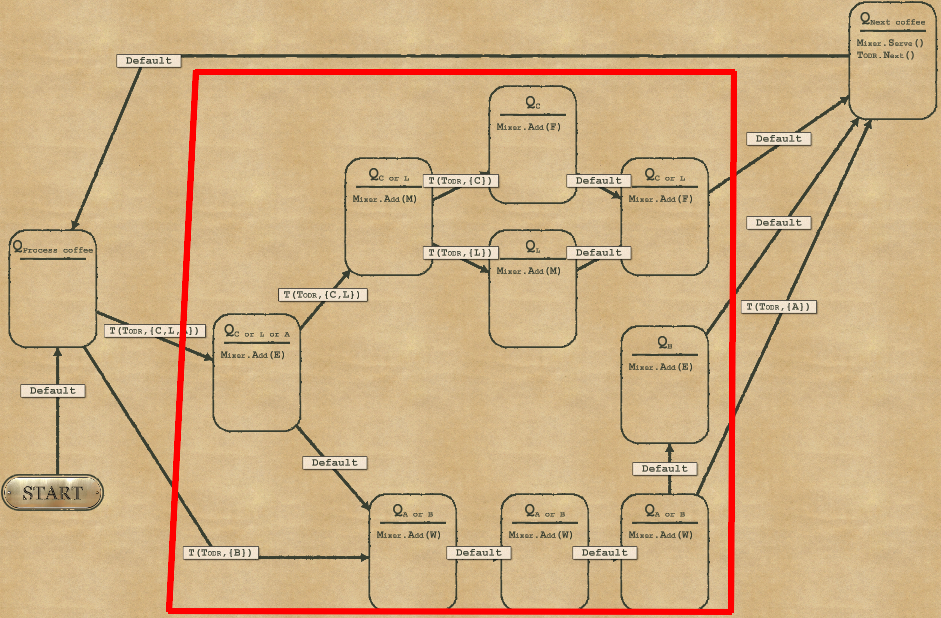
2-3 Grouphead

Let’s start with a solution for Complexity.
 
 

 

• The highlighted part in red is simply adding the 4 consecutive ingredients needed for the current coffee, with some optimizations (for instance Capuccino and Latte have only 1 ingredient which is different, so the path is pretty much the same except that ingredient. But you know that already from the previous chapters).
• The part to the left is the starting point of each new coffee, ready to dispatch the task to the sequence that will handle teh ingredients
• The part to the top right is serving the coffee and moving on to the next one (remember you can set 2 actions in a single node if they’re operated on different devices)

 
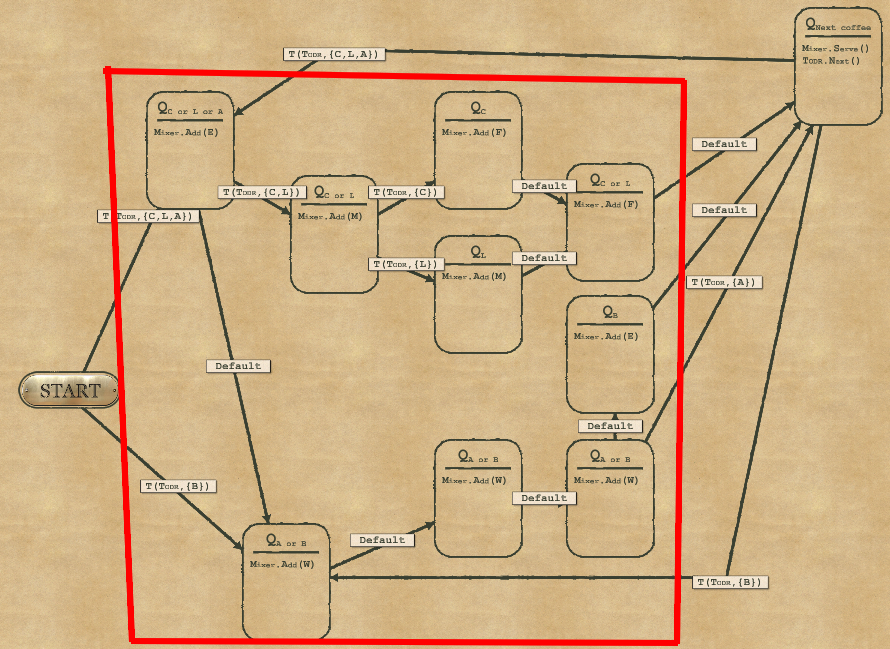
So what about Speed?
 
But you have probably noticed that the left node is empty. So let’s optimize that further to avoid this unnecessary step. If you have node X going to that empty node, and then going further to node Y then you can replace that by an equivalent condition directly from X to Y. After removing that node, we get the final solution reaching both Complexity and Speed at the same time (I’ve highlighted the same red part as before to help visualize it).
 
 

 
 
 

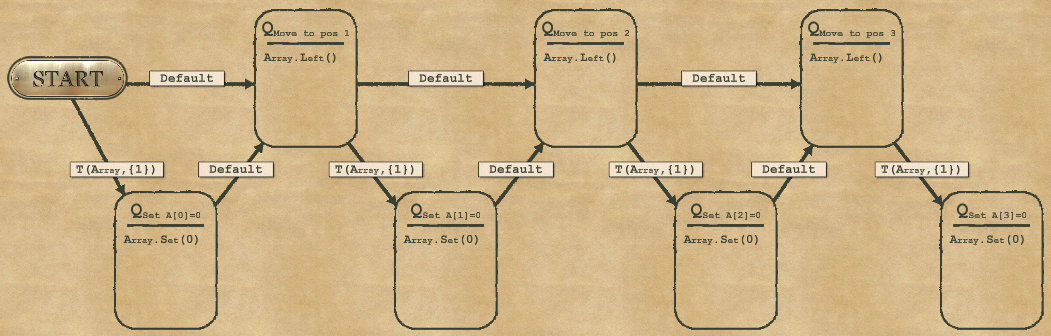
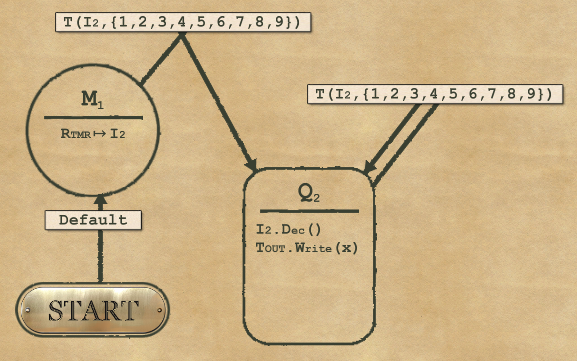
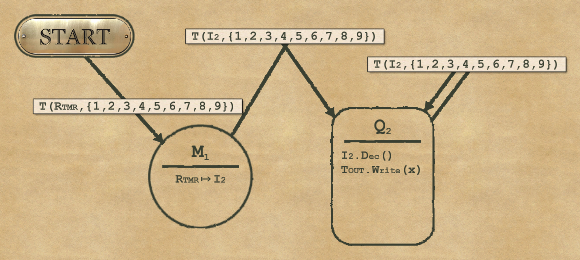
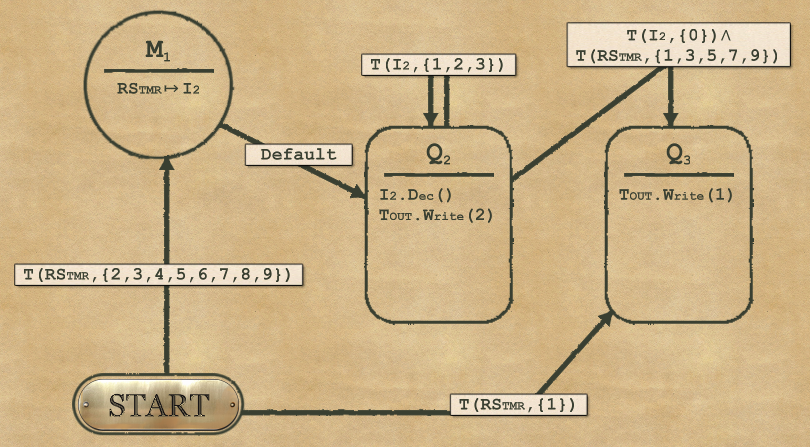
2-4 Timer

For complexity, you can use the new mapper (setting the variable for number of X to write in I2), and then do a loop by decrementing I2.
 
 

 
 
And for Speed, we need to save some operations. This is done by improving the “default” rule and avoid preparing the mapper if unnecessary:
 
 

 
 
I would like to take this opportunity with a not-so-complex puzzle to illustrate a different Speed solution. Maybe not the most elegant, but it’s the fastest. This is called loop unrolling, and it consists in removing every operation used for managing the loop even if it means doing repetitive tasks. In this case the operations that are not strictly necessary would be:
 

• Using the mapper (we can use the RTMR instead)
• Doing the final I2.Dec (no need to decrement it from 1 to 0 because it was the last one)
• And more generally, if we remove the mapper we can remove the counter and I2 as well

So we can “unroll” the loop by writing the Xs one by one. Painful, but it works… and you get a better Speed than actually required.
 
 

 
 
 

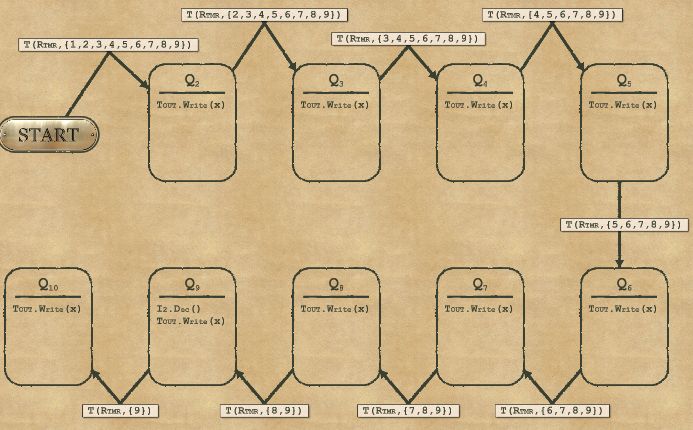
2-5 Pump

This works for both Complexityand Speedat the same time.
 
 

 
For this we use mostly 2 nodes:
 

• Create a mapper with the right value to write which is the computed value for 9-X (0 becomes 9, 1 becomes 8, 2 becomes 7 and so on)
• One node to move on to the next number

And as usual don’t forget to test constantly (using conditions on transitions) if you’ve reached the end, to avoid unnecessary steps.
 
 
 

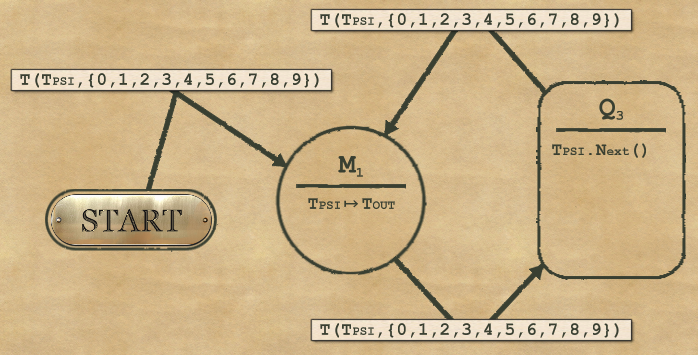
2-6 Heater

This works for both Complexityand Speedat the same time.
 
 

 
Here the idea is to:
 

• prepare a mapper counter in I2 with the number of “2”s that you’re going to write. That means the mapping is (0 and 1 become 0, 2 and 3 become 1, 4 and 5 become 2 and son on…).
• Then add one more node for a loop to write those “2” (with a transition on itself to iterate and a dec counter to know when to stop the loop)
• And one final node to write the “1” if the initial number is even.
   
   
   
   
   
  Don’t forget to use the right condition on every transition to make sure you’re not moving to the next step unless strictly necessary, otherwise you won’t reach the Speed requirement.

 
 
 

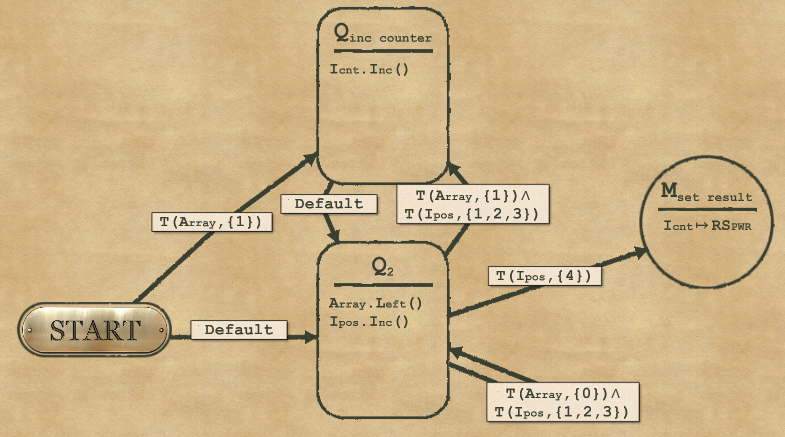
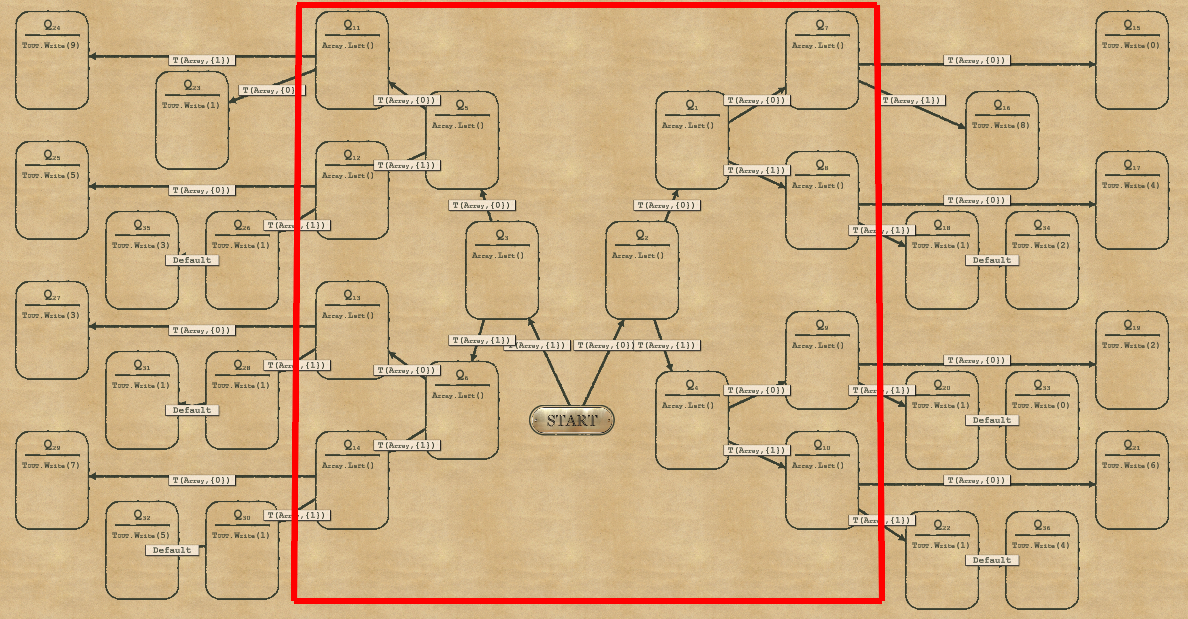
2-7 Main Gearbox

The idea is to iterate over the different positions in the Array (from right to left) and increase a counter every time we find a “1”. For this we’ll need to add:
 

• One integrator Icnt to count the number of “1” that we have already found
• One integrator Ipos to know which is the current position in the Array
• One mapper to copy the result from our Icnt to the expected Rspwr register

At the end we copy the response value from Icnt to the expected Rspwr.
 
 
Let’s start with the complexitysolution:
 
 

 

• We have reached the end of the array (our Ipos has reached value 4), so we go to the last step with the mapper
   
   
   
• We have not reached the end and the current array value is “1” –> we increase the counter before going back to Q2 to move on to the next position
   
   
   
• We have not reached the end and the current array value is “0” –> we go directly to Q2 again to move on to the next position

 
 
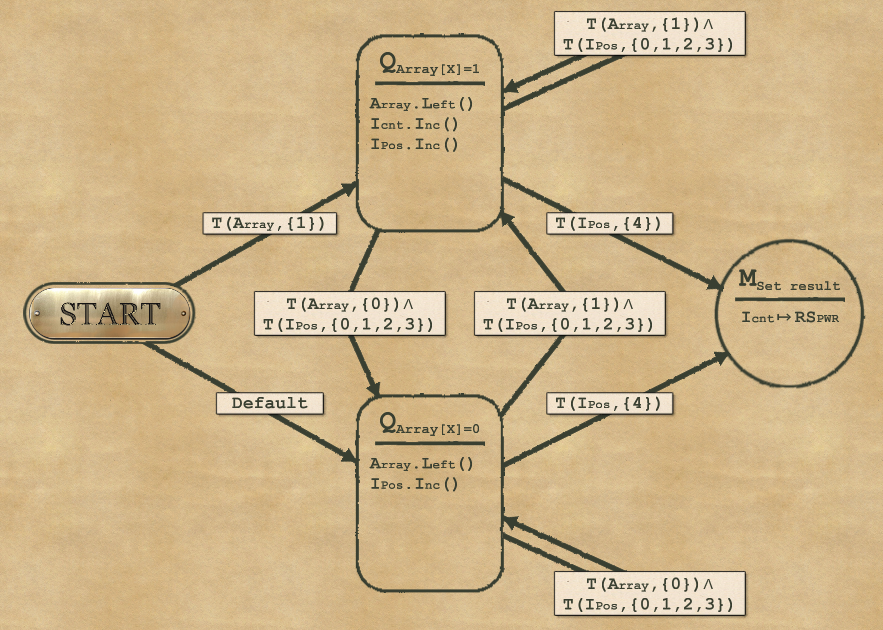
Now the Speedsolution.
 
 

 
In this case we want to minimize the number of transitions especially when we need to increase our Icnt. Instead of having a specific node for increasing the counter (your program had to test if the counter was “1”, then go to the node to increase the counter, then go back to Q2), we use:
 

• One node to handle the current position if its value is 0 (at the bottom on the picture). It will move to the next position (go left + increase Ipos).
• One node to handle the current position if its value is 1 (at the top on the picture). It will increase Ipos AND move to the next position (go left + increase Ipos).

Then it’s mostly a matter of setting the right conditions on each transition to alternate between the top (array=1), the bottom (array=0) or the final mapper when we reach the end.
 
 
 

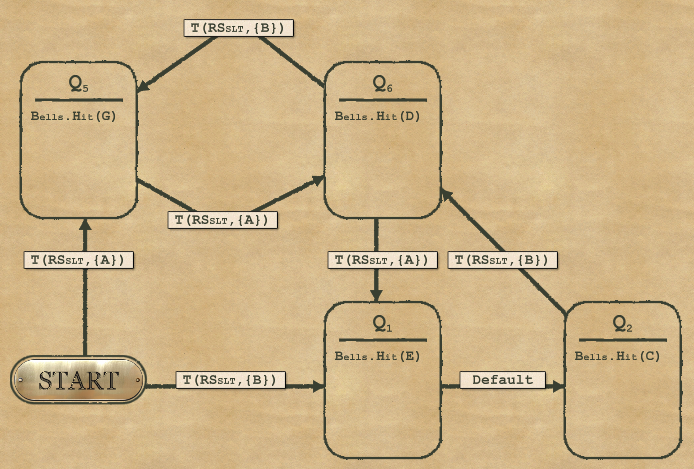
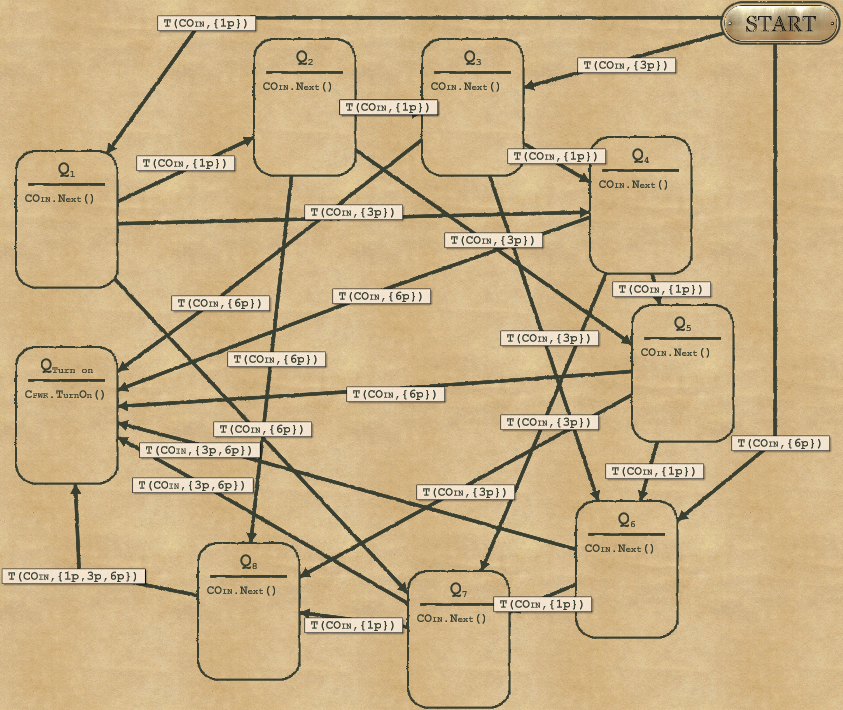
2-8 Coin Mechanism

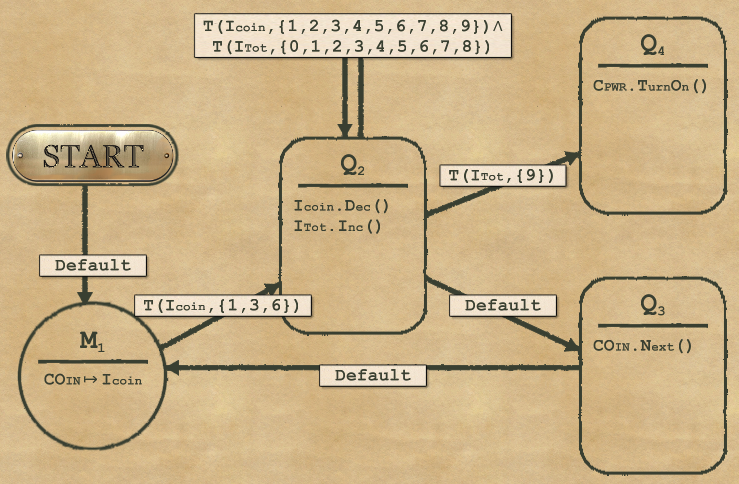
Here’s a solution for Complexity.
 
 

 
This is how it works:
 

• For the current coin, we use a mapper to set the value of the current coin into Icoin. The mapper maps 0 to 0, 1 to 1, 3 to 3 and 6 to 6
   
   
   
• Then the node Q2 increase Itot by the amount in Icoin. We can only increment or decrement, we can’t add values. So we do it with a loop by decreasing Icoin 1 by 1 and increasing Itot 1 by 1 at the same time, until Icoin is 0 (we basically transfer 1 pence at a time from Icoin to Itot)
   
   
   
• Then the node Q3 moves on to the next coin (and we do the same again setting the mapper then transferring to Itot…)
   
   
   
• Finally we need an exit condition to turn on Cpwr. This is done when we reach 9 in Itot.

 
And for Speed
 
This solution for speed is very different from the complexity solution. Here the idea consists in creating a state diagram using nodes where each node represents the number of pence already found.
 
 

 
 
Let’s take an example. The coin sequence is 3,3,1,6,1:
 

• You start at 0 (START).
• Then you find a 3p coin, you switch to the node for 3p (Q3).
• Then you find a 3p coin, so you move to the node 3+3=6 (Q6)
• Then you find a 1p coin, so you move to the node 6+1=7 (Q7)
• Then you find a 6p coin, so you have exceeded 9 and reach the final node to “TURN ON”

 
Note that this solution reaches the previous speed expectations (9.75). With a patch on December 24th, 2022 the puzzle was made easier by increasing the Speed requirement to (20.08).
 
 
 

3-1 Binary Number Converter

Speed

 
First let’s have a look at the simplest (call it dumb if you want) solution which meets the Speed check:
 
 

 
Here we’re testing all possible combinations in the red part, and then we write the results. Extremely fast. Probably the fastest you could build. It works. But definitely boring…
 
 

Complexity

 
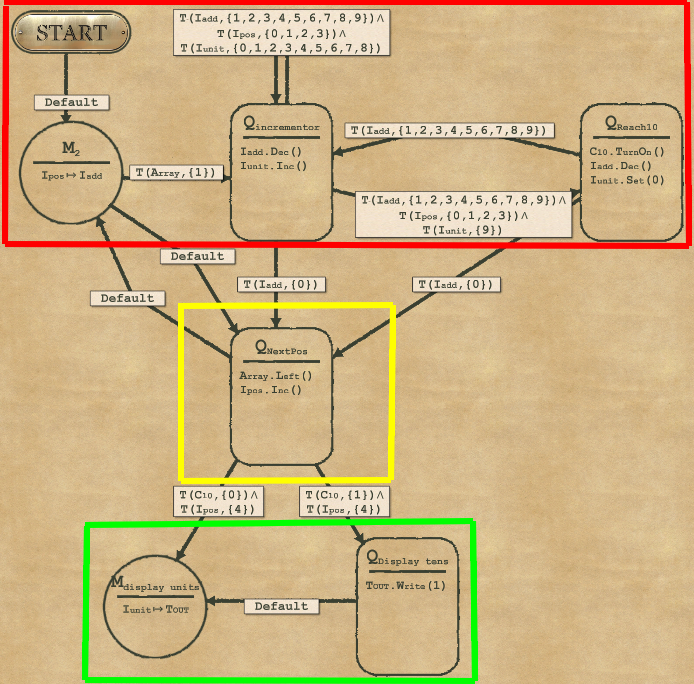
The main idea is to compute the value from the array into a numeric variable, and then display its value.
 
To convert an array into a numeric variable, we’ll have to iterate over each position of the array. And a reminder about binary basics is that the first position is worth 1 (2^0), the second is worth 2 (2^1), the third is worth 4 (2^2) and the fourth is worth 8 (2^3).
 
So we’ll need to add 1,2,4 or 8 respectively to our counter. Remember the previous puzzle where we had to add 1,3 or 6 pence coins? We’ll use the same mechanism.
 
But… the counter we have at our disposal is called Integrator and can only count up to 9, so how to store values up to 15? We can work around that. You may have noticed that there is a maximum of 2 digits to write, as we’re going to write numbers between 0 and 15.
 

• The first digit – if present – is always 1
• The second digit can be anything

That is quite interesting, because the second digit is perfect to fit into our integrator.
 
As for the remaining digit, all we need to remember is if we have reached 10+ or not. And for this we have a boolean variable in the game called Clutch Switch.
 
 
So let’s summarize the devices we need:
 

• Have an integrator Iunit and a clutch switch C10 to represent the final number
• We’ll need to remember which position in the array we’re at. It’ll be Integrator Ipos
• We’ll need to know if we’re adding 1,2,4 or 8. This value will be stored in integrator Iadd

 

 
 
And the final algorithm is:
 

• The mapper which maps the Position (0,1,2,3) to the decimal value it represents (1,2,4,8) to Iadd
   
   
   
• A “pence counter” (called Qincrementor) that increments Iunit and decrements Iadd at the same time until Iadd reaches 0
   
   
   
• In case Iunit is maxed, the “Qreach10” node will turn on the C10 switch and reset the Iunit counter

 
 

 
 
Hope you enjoy the post for Alan’s Automaton Workshop Solving Automatons for Complexity or Speed, If you think we should update the post or something is wrong please let us know via comment and we will fix it how fast as possible! Thank you and have a great day!