This guide is intended to assist with changes in periscope scaling, and distance measurement in version 0.26.

Prologue

The scaling of the periscopes underwent significant changes in version 26, a significant step toward historical authenticity. This change made determining the distance to the target ships a little more difficult, which caused a mixed reaction from players. But Wolfpack became one the few submarine-themed games in the world where the scaling for the periscopes matches the historical one. This guide was created to make it easier for players to sink ships. Let’s be clear: this guide only covers vertical distance determination. Horizontal ranging and the trigonometry involved will be covered in another guide.

The Past

Presumably, everyone is familiar with these terms: milliradian, centiradian. These terms refers to the hundredths, or the thousandths, of a Radian using metric prefixes. They represent the distance between the small lines visible through the periscope. The distance between two lines is 1 centiradian (10 milliradians).

One centiradian equals one meter viewed from 100m away. It was very easy to use and calculate because it used the metric number system and most of the full numbers, or maybe one decimal.

This is no longer valid in version 0.26

The Present, The Math and the Great Dispute

The scale of one miliradian has been changed to one-sixteenth. Although the /16 mark was present in earlier versions of the periscope optics, the actual change was only made to version 0.26. The change is only 10% from the centiradian that was previously used. Players who still use the old formulas will still be able sink ships but with a significantly lower accuracy. To understand the changes in scaling, we must examine the difference between degree- and radian unit.

The radian (symbol: rad) is the SI unit for measuring angles, and is the standard unit of angular measure used in many areas of mathematics. One radian is the angle which intersects an arc that is equal in length to its radius from the circle’s center. The SI defines the Radian as a dimensionless unit having 1 rad = 1.

A degree or arc degree (deg, symbol: deg ) is a measurement of a plane angle in which one full rotation is 360 degrees. It is not an SI unit (radian it), but it is accepted in the SI Brochure.

This is how you can convert radian to degree:

1° = (π/180) rad

In which:

1° = 0.01745 rad

Let’s take a look at Wolfpack and our Periscope to see how this will turn out. We stated previously that the scaling of periscopes changed to 1/16deg in version 0.26.

1/16° = 0.0625°

Let’s convert it to radians.

0.0625° = 0.001090831 rad

Or, if you use a prefix

1.0908 milliradians

Practically, this means that we must convert the degrees visible in the scope into radians. Radians can be used for distances expressed in SI meters or prefixes with hectometers and kilometers. You can convert within the formulas. Let’s first establish the mathematical rule that multiplication is easily converted to division by using the reciprocal one of the numbers. Multiplication or division will depend on how easy it is to find the solution. Using this rule, convert the conversion number 1.0908 into a multiplier. The reciprocal of 1.0908 would be:

1 / 1.0908 = 0.9168

Do not lose heart, we are making progress!

These two numbers will play a significant part in determining the distance. It all depends on which formula is easiest for which player. Multiplication is generally used more often by people, but this is determined by individual preference.

These are the numbers:

 

1.0908
0.9168

You might wonder what to call the small lines between the periscope’s periscope’s lines if they moved from centiradian, milliradian, or 1/16th of an inch? It is officially called 1/16th degree. But it’s not too complicated, right? There are many solutions, but no consensus. The Great Dispute. Lines, marks and ticks, bar signs, signs, and so many players, so many names. You can call it whatever you like, but the important thing is that the crew understands what your talking about. Don’t forget to share any historical documents that include the name Gunther Kretchmer, or Otto Kretchmer calling the name it. I will use marks in this guide.

Data collection

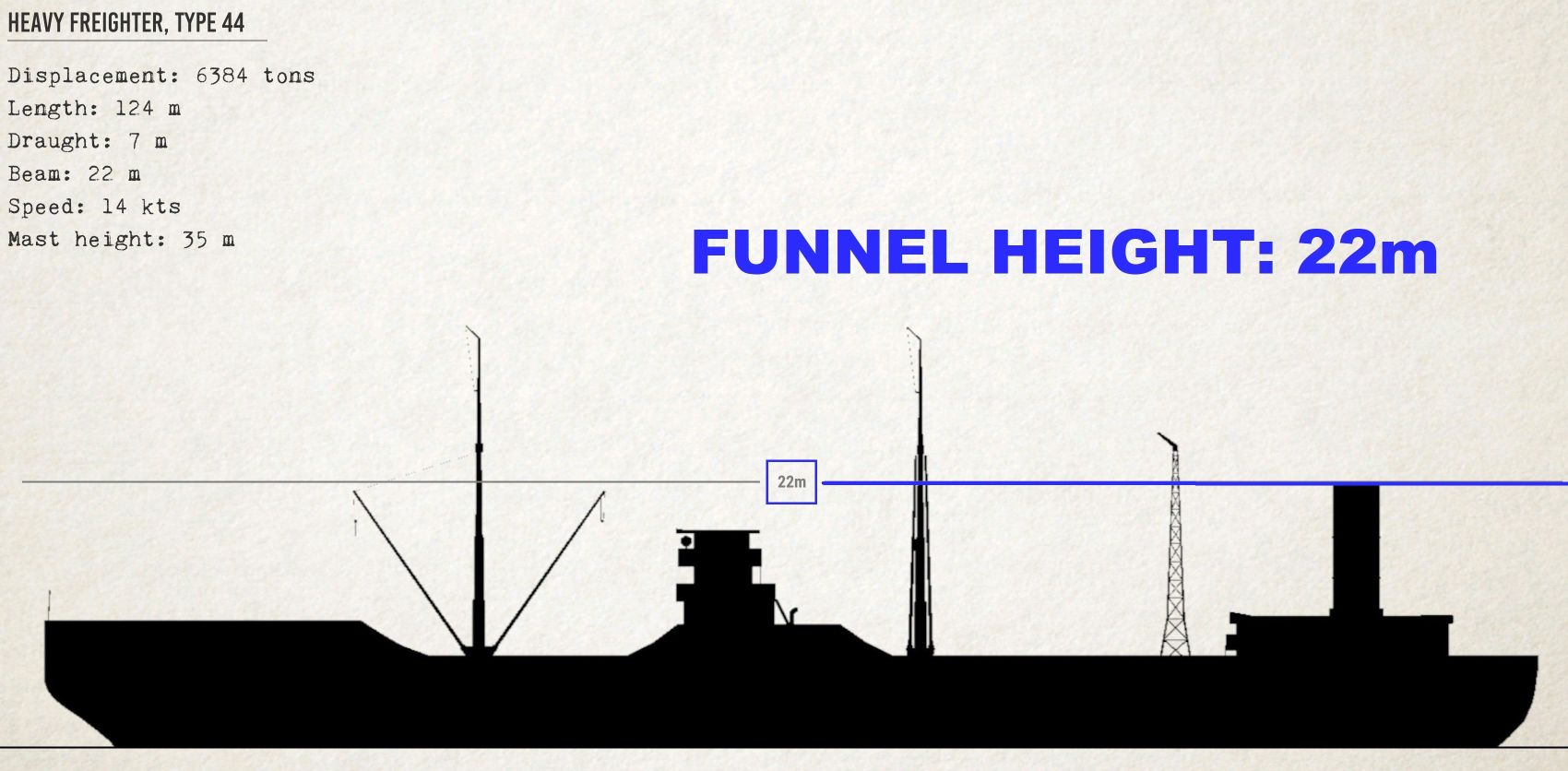
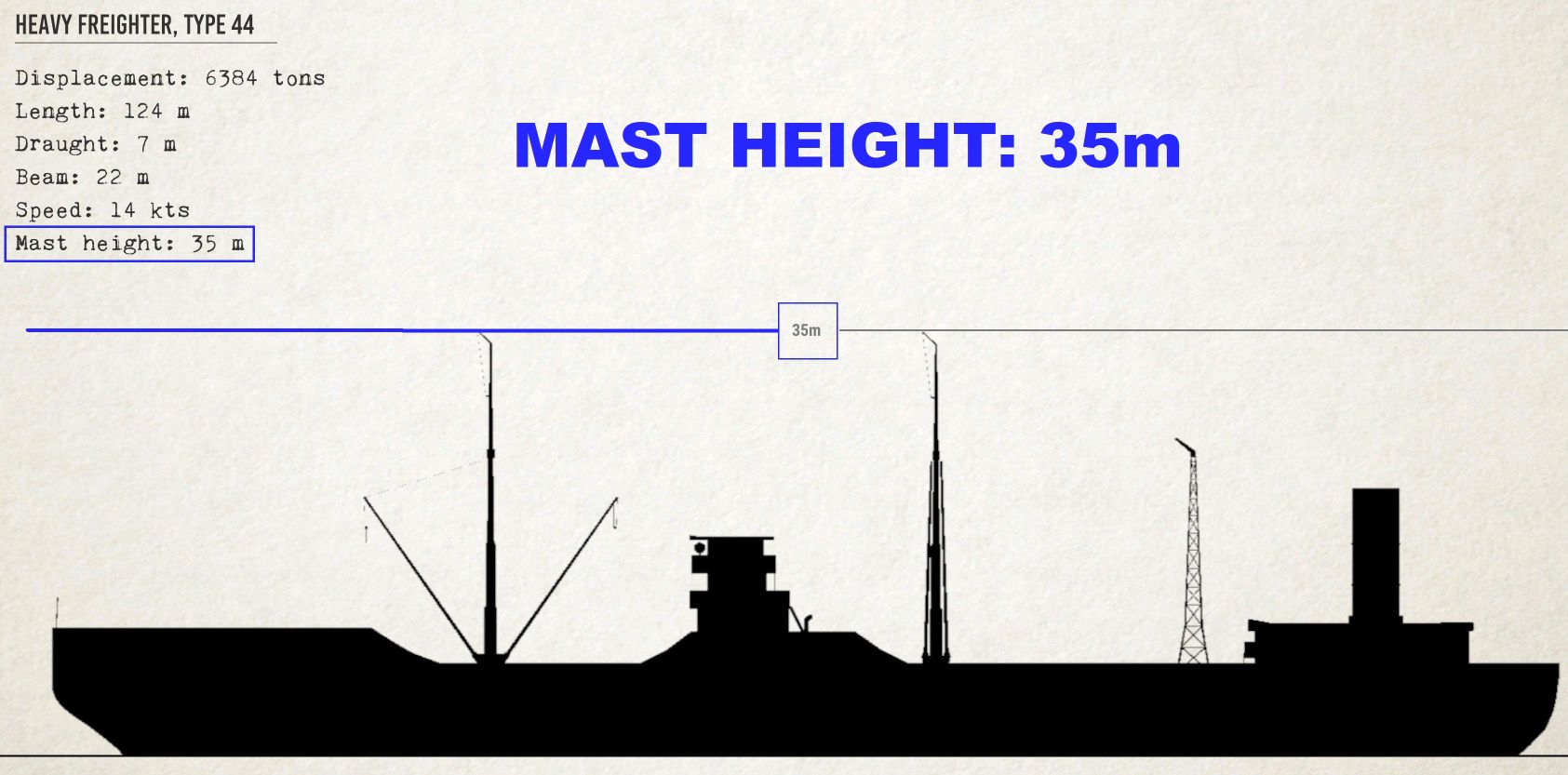
Later on, we will require data such as heights and periscope marks. The feature used on the target will affect the height. This can be the maximum mast elevation, which is indicated for each ship by the Recognition Manual. Or, we may use a portion or the funnel of the mast.

Any solution can be used for this purpose. However, the more detailed the measurement, the better. To count the number and location of markings, place horizontal line of periscope on ship’s waterline. Then count the number of vertical lines on the left-hand side of periscope. You can also place the horizontal line at or near the top of the feature. The lines can then be counted to the waterline. The 50th line will be indicated by the 5th line either downwards or upwards.

If you multiply the distance between two marks by 10 (old milliradian method), you will get kilometers. You will get hectometers by counting it as 1 (old-centiradian method).

Technically they are the same, but it is important that you put the right value into TDC.

It’s using hectometers!

Formulas

One of the two numbers above can be used to compensate for the change in periscope scale. If it seems difficult at first, don’t despair. We will simplify it completely at the end.

But let’s not forget about one important fact. The periscopes offer 1.5x and 6x zoom levels. These must be considered when formulas are used. The difference between these zoom levels is 4x, i.e. 1.5 x 4 = 6.

Let’s start with new formulas that include the conversion numbers.

1.5x ZOOM

 

Range = height / (marks * 1.0908)

Or

Range = height / (marks * 0.9168)

In the first formula, conversion numbers were used as a quotient. The second formula used them as multipliers. We will see that it doesn’t really matter which version you use. The essence lies in how the operations are done in the formula.

Let’s suppose that the mast height at 30m is the case and that the periscope marks at 22 are the case.

30 / (22 * 1.0908) = 1.25 km

Or

30 / 22 * 0.9168 = 1.25 km

You should not be alarmed if the results you receive are slightly different. This is because the conversion numbers are rounded. The difference will not affect accuracy as it is so small. If you want to get the final results in kilometers instead of in hectometers which are required for the TDC, then you will need to use a decimal place in the number periscope markings (2.2 in this example instead of 22).

Let’s look at 6x zoom. The difference in zoom levels is 4x. Therefore, we need to add a 4x multiplier above the formulas.

6x ZOOM

Range = (height * 4) / (marks * 1.0908)

Or

Range = (height / marks) * 0.9168 * 4

Let’s look at an example: height 30m, periscope marks 22,

(30 * 4 = / (22*1.0908 – = 5.km

30 / (22 * 4 * 0.9168 = 5.0 km

Mathematics has a special property. A rule that says that if a multiplication/division consists of multiple terms, they can be multiplied/divided with each other. This will result in a constant amount in our formula being modified but with one less term.

We will start with a very basic example.

5 * 5 * 5 = 125

We can simplify

5 * 25 = 125

By multiplying two numbers together. This is the concept that we’re going next.

In our case, both the 4x multiplier (and the conversion numbers 1.0908/0.9168) are constant. Let’s simplify these formulas.

4 / 1.0908 = 3.667
4 * 0.9168 = 3.667

In both cases, the same number is returned which is:

3.667

Let’s see how these formulas develop using the same example data.

30 * 3.667/22 = 5.0 km

30 / 22 / 3.667 = 5.0 km

As you can see our formula for 6x zoom was simplified to use height, perscope marks, and a new constant – the magic number of 3667. The formulae will look the following when you use the new constant:

Range = height * 3.667 / marks

Or

Range = height / marks * 3.667

Simply put, the old multiplier of 4x used to 6x zoom level must be changed to 3.667

Simple!

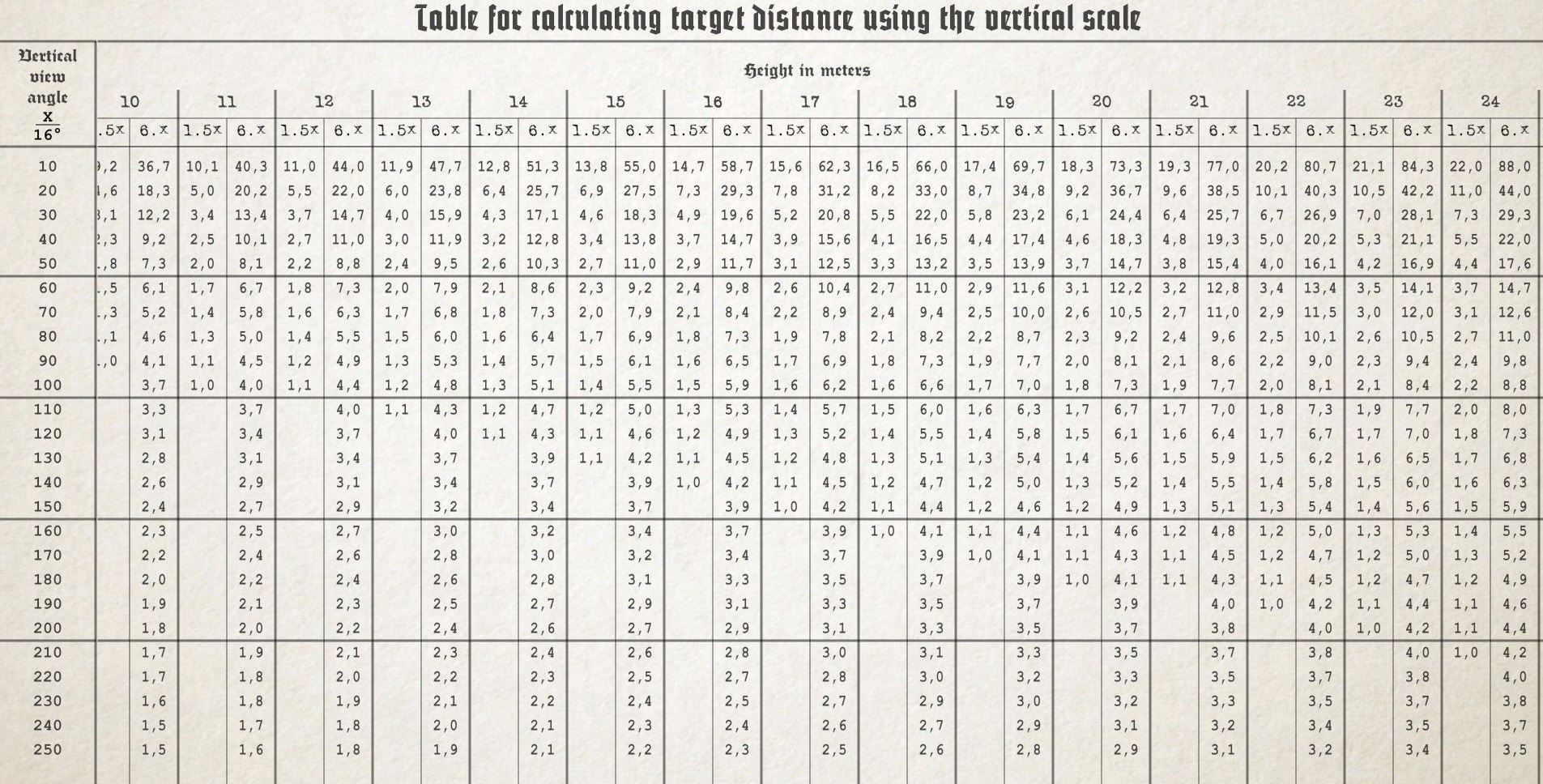
Tables and overlay

The Distance Table is a tool that can be used to calculate distances without the need for formulas. The Distance Table can also be found in C menu. You can also bring up the overlay in the periscope with the set hotkey. You can adjust the height of the overlay by using the set hotkeys. Or by 10 by setting the zoom level. You can switch between horizontal or vertical distances using the appropriate hotkey. Updated versions of the Distance Table as well as the overlay have been released. These are both immediately available and simple to use. Their drawback is their inaccuracy. However, they are not exact for markings 20, 30, 40 and so on. However, if there are more than 25 periscope marks, then the intermediate value must either be calculated or guessed from memory. This guide was created in order to eliminate any inaccuracies. It calculates everything manually so that we can get accurate impact times. This is essential and necessary for coordinated attacks.

Final words

The author hopes the guide will be helpful in manual distance measurement. This only requires a basic calculator. It takes only a few seconds to calculate, which won’t slow down the gameplay but will improve the experience. I struggled to understand the change in version 0.26 initially, but I was helped by some brilliant minds to get it sorted out and be able to help others. I would like to thank all those who helped me with these matters, as well as those who have read this guide.

Happy hunting, sailor!

—————————————————–

 

Hope you enjoy the post for Wolfpack Prologue Manual Ranging in 0.26+, If you think we should update the post or something is wrong please let us know via comment and we will fix it how fast as possible! Thank you and have a great day!